programmers.co.kr/learn/courses/30/lessons/72413?language=python3
코딩테스트 연습 - 합승 택시 요금
6 4 6 2 [[4, 1, 10], [3, 5, 24], [5, 6, 2], [3, 1, 41], [5, 1, 24], [4, 6, 50], [2, 4, 66], [2, 3, 22], [1, 6, 25]] 82 7 3 4 1 [[5, 7, 9], [4, 6, 4], [3, 6, 1], [3, 2, 3], [2, 1, 6]] 14 6 4 5 6 [[2,6,6], [6,3,7], [4,6,7], [6,5,11], [2,5,12], [5,3,20], [2,4
programmers.co.kr
최단거리 문제에 대한 알고리즘 종류에 따라 적용해보며 어떤 방법이 가장 효율적인지 확인해보고자 한다.
1. 플로이드 와샬(Floyd_Warshall)
모든 Node 사이의 최단 경로(가중치)를 비교하여 모든 경로에 대한 데이터를 얻을 수 있지만 O(N^3)의 시간복잡도를 가진다.
Code에 대해서 간단하게 설명하면, 3개의 For문으로 구성하여 전체 경우에 수에 대한 분석이 가능하다.
2개의 For문으로 전체 Node 사이에 대한 값을 뽑고, 남은 1개의 For문으로 중간에 다른 Node가 포함됐을 때의 데이터도 비교하는 방식이다.
#플로이드 와샬(Floyd-Warshall)
def solution(n, s, a, b, fares):
inf_v = 20000001 #fare 최대 10만,n 최대 200
graph =[[inf_v]*n for i in range(n)]
temp = inf_v
#data 정리
for arr in fares:
graph[arr[0]-1][arr[1]-1]=arr[2]
graph[arr[1]-1][arr[0]-1]=arr[2]
#플로이드 와샬
for t in range(len(graph)): # t : 중간에 Node가 있을 경우 확인하기 위함
for i in range(len(graph)): # i,j : 전체 데이터 출력을 위함
for j in range(i, len(graph)):
if i!=j:
graph[i][j] = graph[j][i] = min(graph[i][j],graph[i][t]+graph[t][j])
if i==j: graph[i][j]=graph[j][i]=0
for t in range(n):
temp = min(temp,graph[s-1][t]+graph[t][a-1]+graph[t][b-1])
answer = temp
return answer
n= 6
s= 4
a= 6
b= 2
fares= [[4, 1, 10], [3, 5, 24], [5, 6, 2], [3, 1, 41], [5, 1, 24], [4, 6, 50], [2, 4, 66], [2, 3, 22], [1, 6, 25]]
print(solution(n, s, a, b, fares))
2. 다익스트라 알고리즘 (Dijkstra's Algorithm)
플로이드 와샬과 다르게 단일 Node에 대한 최단 경로를 구할 수 있다. 이번 문제의 경우 가장 적은 비용을 구하는 문제이기 때문에 다익스트라 알고리즘 사용하는게 효율성 측면에서 높은 이점을 가진다. O((V+E)logV)의 시간복잡도를 가진다.(V : 전체 Node수, E : 인접한 Node수)
heapq를 이용하여, 가장 작은 수만 뽑아내는 방식이다. Code 자체가 직관적으로 이해하기가 어려워 이해하는 꼬박 하루를 썼다. 말로 설명이 어렵지만, 간단하게라도 정리해보려고 한다.
1) graph 그리기
graph 그리는 것은 플로이드 와샬과 비슷한 방식이나, Node(x,y)와 Fare(z)를 정리할때 비용(z)를 먼저 써서 정리하였다. 이 이유는 우리가 Heapq 모듈을 사용하기 위함인데, Heaqp의 경우 정렬과 다르게 항상 0번 열에 최소값이 나오게 정리하게 된다. 우리가 원하는건 Fare를 최소하는게 목적이기 때문에 Fare로 정렬 될 수 있도록 z를 기준으로 Graph를 만들었다.
graph = [[] for _ in range(n)]
for x,y,z in fares:
graph[x-1].append((z,y-1))
graph[y-1].append((z,x-1))
print(graph)
#결과 :
# [[(10, 3), (41, 2), (24, 4), (25, 5)],
# [(66, 3), (22, 2)],
# [(24, 4), (41, 0), (22, 1)],
# [(10, 0), (50, 5), (66, 1)],
# [(24, 2), (2, 5), (24, 0)],
# [(2, 4), (50, 3), (25, 0)]]2) Dijkstra's Algorithm
목적지와 도착지 사이에 최소 비용(최소 거리)를 뽑아내기 위해서 1차적으로 시작하는 Node하나와 그에 상응하는 Fare값을 넣어 Heapq에 원소로 넣어준다. 이제 주변 Node와 비교하기 위해서 For문을 구성하고, 선정한 Node와 연결된 Node와 비교하여 최소 비용을 검토하게 된다.
이때 플로이드 와샬과 큰 차이점으로 플로이드 와샬은 전체 Node간 최소 비용을 나타내지만 다익스트라는 시작하는 Node 하나에서 다른 Node간에 최소 비용을 나타낸다. 결과적으로 플로이드 와샬의 결과는 2차원 배열, 다익스트라는 1차원 배열로 값이 나오게 된다.
import heapq
def solution(n, s, a, b, fares):
graph = [[] for _ in range(n)]
for x,y,z in fares:
graph[x-1].append((z,y-1))
graph[y-1].append((z,x-1))
inf_v=20000001
temp_sum = []
for tr in range(n):
q=[(0,tr)]
visit=[True]*len(graph)
dp = [float('inf')]*len(graph)
dp[tr]=0 # transfer위치 잡기
while q:
fare,destin = heapq.heappop(q)
if visit[destin] == True:
visit[destin]=False
for value,key in graph[destin]:
if dp[key] > value + dp[destin]:
dp[key] = value + dp[destin]
heapq.heappush(q,(dp[key],key))
temp_sum.append(dp[a-1]+dp[b-1]+dp[s-1])
answer = min(temp_sum)
return answer 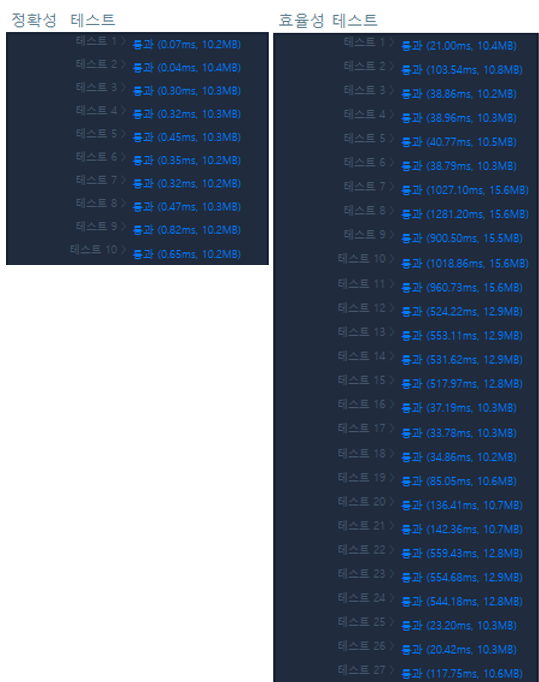
결론
이번 문제는 플로이드 와샬, 다익스트라 알고리즘 두 가지 방식으로 문제를 풀어 보았다. 확실히 효율성은 다익스트라 알고리즘에서 우수한 것을 확인하였는데, 효율성 시간이 들쭉 날쭉한것으로 보아, 경우에 따라 효율성이 나빠질 수도 있어보이는데, 추가적으로 공부가 필요할 것 같다.
이번 문제는 음의 가중치가 없기 때문에 Circle이 만들어질 염려가 없었지만, 만약 음의 가중치가 있을 경우에 상기 방식으로는 안풀릴 수 있다. 그럴때는 벨만-포드 알고리즘을 활용하여 진행이 필요하다고 하는데, 이 부분도 더 공부가 필요할 것 같다.
'Coding > 코테' 카테고리의 다른 글
| [백준 1463] 1로 만들기(python) (0) | 2024.07.26 |
|---|---|
| [프로그래머스] 2021 카카오 공채 - 큰 수 만들기 (파이썬) (0) | 2021.04.25 |
| [프로그래머스] 2021 카카오 공채 - 정수 삼각형 (파이썬) (0) | 2021.04.25 |
| [프로그래머스] 2021 카카오 공채 - 카드 짝 맞추기 (파이썬) (0) | 2021.04.22 |
programmers.co.kr/learn/courses/30/lessons/72413?language=python3
코딩테스트 연습 - 합승 택시 요금
6 4 6 2 [[4, 1, 10], [3, 5, 24], [5, 6, 2], [3, 1, 41], [5, 1, 24], [4, 6, 50], [2, 4, 66], [2, 3, 22], [1, 6, 25]] 82 7 3 4 1 [[5, 7, 9], [4, 6, 4], [3, 6, 1], [3, 2, 3], [2, 1, 6]] 14 6 4 5 6 [[2,6,6], [6,3,7], [4,6,7], [6,5,11], [2,5,12], [5,3,20], [2,4
programmers.co.kr
최단거리 문제에 대한 알고리즘 종류에 따라 적용해보며 어떤 방법이 가장 효율적인지 확인해보고자 한다.
1. 플로이드 와샬(Floyd_Warshall)
모든 Node 사이의 최단 경로(가중치)를 비교하여 모든 경로에 대한 데이터를 얻을 수 있지만 O(N^3)의 시간복잡도를 가진다.
Code에 대해서 간단하게 설명하면, 3개의 For문으로 구성하여 전체 경우에 수에 대한 분석이 가능하다.
2개의 For문으로 전체 Node 사이에 대한 값을 뽑고, 남은 1개의 For문으로 중간에 다른 Node가 포함됐을 때의 데이터도 비교하는 방식이다.
#플로이드 와샬(Floyd-Warshall)
def solution(n, s, a, b, fares):
inf_v = 20000001 #fare 최대 10만,n 최대 200
graph =[[inf_v]*n for i in range(n)]
temp = inf_v
#data 정리
for arr in fares:
graph[arr[0]-1][arr[1]-1]=arr[2]
graph[arr[1]-1][arr[0]-1]=arr[2]
#플로이드 와샬
for t in range(len(graph)): # t : 중간에 Node가 있을 경우 확인하기 위함
for i in range(len(graph)): # i,j : 전체 데이터 출력을 위함
for j in range(i, len(graph)):
if i!=j:
graph[i][j] = graph[j][i] = min(graph[i][j],graph[i][t]+graph[t][j])
if i==j: graph[i][j]=graph[j][i]=0
for t in range(n):
temp = min(temp,graph[s-1][t]+graph[t][a-1]+graph[t][b-1])
answer = temp
return answer
n= 6
s= 4
a= 6
b= 2
fares= [[4, 1, 10], [3, 5, 24], [5, 6, 2], [3, 1, 41], [5, 1, 24], [4, 6, 50], [2, 4, 66], [2, 3, 22], [1, 6, 25]]
print(solution(n, s, a, b, fares))
2. 다익스트라 알고리즘 (Dijkstra's Algorithm)
플로이드 와샬과 다르게 단일 Node에 대한 최단 경로를 구할 수 있다. 이번 문제의 경우 가장 적은 비용을 구하는 문제이기 때문에 다익스트라 알고리즘 사용하는게 효율성 측면에서 높은 이점을 가진다. O((V+E)logV)의 시간복잡도를 가진다.(V : 전체 Node수, E : 인접한 Node수)
heapq를 이용하여, 가장 작은 수만 뽑아내는 방식이다. Code 자체가 직관적으로 이해하기가 어려워 이해하는 꼬박 하루를 썼다. 말로 설명이 어렵지만, 간단하게라도 정리해보려고 한다.
1) graph 그리기
graph 그리는 것은 플로이드 와샬과 비슷한 방식이나, Node(x,y)와 Fare(z)를 정리할때 비용(z)를 먼저 써서 정리하였다. 이 이유는 우리가 Heapq 모듈을 사용하기 위함인데, Heaqp의 경우 정렬과 다르게 항상 0번 열에 최소값이 나오게 정리하게 된다. 우리가 원하는건 Fare를 최소하는게 목적이기 때문에 Fare로 정렬 될 수 있도록 z를 기준으로 Graph를 만들었다.
graph = [[] for _ in range(n)]
for x,y,z in fares:
graph[x-1].append((z,y-1))
graph[y-1].append((z,x-1))
print(graph)
#결과 :
# [[(10, 3), (41, 2), (24, 4), (25, 5)],
# [(66, 3), (22, 2)],
# [(24, 4), (41, 0), (22, 1)],
# [(10, 0), (50, 5), (66, 1)],
# [(24, 2), (2, 5), (24, 0)],
# [(2, 4), (50, 3), (25, 0)]]2) Dijkstra's Algorithm
목적지와 도착지 사이에 최소 비용(최소 거리)를 뽑아내기 위해서 1차적으로 시작하는 Node하나와 그에 상응하는 Fare값을 넣어 Heapq에 원소로 넣어준다. 이제 주변 Node와 비교하기 위해서 For문을 구성하고, 선정한 Node와 연결된 Node와 비교하여 최소 비용을 검토하게 된다.
이때 플로이드 와샬과 큰 차이점으로 플로이드 와샬은 전체 Node간 최소 비용을 나타내지만 다익스트라는 시작하는 Node 하나에서 다른 Node간에 최소 비용을 나타낸다. 결과적으로 플로이드 와샬의 결과는 2차원 배열, 다익스트라는 1차원 배열로 값이 나오게 된다.
import heapq
def solution(n, s, a, b, fares):
graph = [[] for _ in range(n)]
for x,y,z in fares:
graph[x-1].append((z,y-1))
graph[y-1].append((z,x-1))
inf_v=20000001
temp_sum = []
for tr in range(n):
q=[(0,tr)]
visit=[True]*len(graph)
dp = [float('inf')]*len(graph)
dp[tr]=0 # transfer위치 잡기
while q:
fare,destin = heapq.heappop(q)
if visit[destin] == True:
visit[destin]=False
for value,key in graph[destin]:
if dp[key] > value + dp[destin]:
dp[key] = value + dp[destin]
heapq.heappush(q,(dp[key],key))
temp_sum.append(dp[a-1]+dp[b-1]+dp[s-1])
answer = min(temp_sum)
return answer 
결론
이번 문제는 플로이드 와샬, 다익스트라 알고리즘 두 가지 방식으로 문제를 풀어 보았다. 확실히 효율성은 다익스트라 알고리즘에서 우수한 것을 확인하였는데, 효율성 시간이 들쭉 날쭉한것으로 보아, 경우에 따라 효율성이 나빠질 수도 있어보이는데, 추가적으로 공부가 필요할 것 같다.
이번 문제는 음의 가중치가 없기 때문에 Circle이 만들어질 염려가 없었지만, 만약 음의 가중치가 있을 경우에 상기 방식으로는 안풀릴 수 있다. 그럴때는 벨만-포드 알고리즘을 활용하여 진행이 필요하다고 하는데, 이 부분도 더 공부가 필요할 것 같다.
'Coding > 코테' 카테고리의 다른 글
| [백준 1463] 1로 만들기(python) (0) | 2024.07.26 |
|---|---|
| [프로그래머스] 2021 카카오 공채 - 큰 수 만들기 (파이썬) (0) | 2021.04.25 |
| [프로그래머스] 2021 카카오 공채 - 정수 삼각형 (파이썬) (0) | 2021.04.25 |
| [프로그래머스] 2021 카카오 공채 - 카드 짝 맞추기 (파이썬) (0) | 2021.04.22 |
